Теория Ф. Шмидта: границы бухгалтерского баланса как арифметического равенства

Теория Ф. Шмидта: границы бухгалтерского баланса как арифметического равенства

Баланс как арифметическое равенство

Рассказывая вам, уважаемые читатели, об истории формирования современного бухгалтерского баланса как финансовой модели экономической единицы, мы не случайно довольно подробно остановились на периоде формирования практики ведения учета методом двойной записи. Комментируя положения знаменитого труда Л. Пачоли (см. № 9 (сентябрь) «БУХ.1С» за 2012 год, стр. 40), мы постарались показать первичную проверочную роль баланса:

• как описи незакрывшихся счетов на конец периода, реализация которой на практике постепенно привела к пониманию равенства
  А - О = К,
  где А - активы, имущество; О - обязательства, долги перед кредиторами; К - собственный капитал или капитал собственников фирмы;

• как арифметического уравнения, решение которого при введении в него прибыли или убытка в качестве искомого неизвестного позволяет представить финансовое положение предприятия и исчислить финансовый результат его деятельности.

Осмысление такой роли баланса и в теории, и в практике бухгалтерского учета постепенно трансформировало рассуждения о балансе как следствии ведения двойной записи на счетах в балансовую теорию учета. Теперь уже сама двойная запись рассматривалась как метод фиксации хозяйственных фактов, позволяющих сформировать баланс. В свою очередь, содержание баланса как простейшей арифметической модели фирмы задавало правила ведения записей на счетах бухгалтерского учета.

Уравнения Шера

Наиболее яркой работой, представившей эту точку зрения, стала книга И.Ф. Шера «Бухгалтерия и баланс» ([1]), о которой мы вели разговор в статье, опубликованной в номере 12 (декабрь) «БУХ.1С» за 2012 год, стр. 33.

Определяя равенство актива и пассива бухгалтерского баланса как «балансовое уравнение» ([1], стр. 19) А = П, где А - актив; П - пассив, Иоган Фридрих Шер (1846-1924) утверждал, что «самую сущность бухгалтерии» при этом выражает «капитальное уравнение»:

А - П = К,

где П - пассив «в собственном смысле», то есть долги предприятия, а К - собственный капитал или «чистое имущество» ([1], стр. 19).

Возможные типы изменений баланса при отражении хозяйственных фактов фирмы Шер разделил на три группы:

1) меновые процессы;

2) операции, приносящие прибыль или убыток;

3) сложные операции.

«Операции, представляющие собой меновые процессы, - писал Шер, - применительно к основному уравнению А - П = К, можно изобразить в виде следующих уравнений:

а) Обмен части актива ан  на другую равноценную часть актива ан:

А + ан - ан - П =К.

б) Уплата долга (выделение пн из актива для погашения пассива пн):

(А - пн) - (П - пн) = К.

в) Покупка в кредит (как актив, так и пассив увеличиваются на ам):

(А + ам) - (П + ам) = К.

г) Превращение одного долга в другой (долги увеличиваются в одной категории на пм и уменьшаются в другой категории на пм):

А - (П + пм - пм) = К» ([1], стр. 23).

«Хотя, - отмечал Шер, - при совершении всех этих хозяйственных операций не оказывается никакого влияния на размеры капитала, как это легко видеть, но они имеют большое значение для внутреннего строения и состава частей имущества и поэтому их надлежит выражать в числах» ([1], стр. 23).

Под «операциями, приносящими прибыль или убыток» Шер понимал те хозяйственные факты, «которые вызывают не только изменение составных частей имущества, но одновременно с этим и изменение величины чистого имущества; это имеет место всякий раз, когда не воспоследует замены выбывающей в результате потребления, уничтожения или потери составной части имущества; или когда вследствие доходности или производительности в хозяйство входит новая стоимость, за которую не дается никакой компенсации... Здесь увеличивается или уменьшается не только величина частей имущества, но также, само собою разумеется, и чистое имущество, как это видно из следующих уравнений, выводимых из основного уравнения А - П = К» ([1], стр. 23-24).

«а) Приход нового блага пр:

А + пр - П = К + пр.

б) Выбытие блага у:

(А - у) - П = К - у.

в) Возникновение нового долгового обязательства пн без активной компенсации:

А - (П + пн) = К - пн.

г) Аннулирование долгового обязательства пн (вследствие дарения, скидки и т. п.):

А - (П - пн) = К + пн» ([1], стр. 24).

Относительно третьей группы фактов - «сложных операций», к которым Шер относил «меновые и прибыльные или убыточные сделки», он отмечал, что «именно ввиду того, что хозяйственная деятельность может быть часто выражена в числах только посредством происшедших изменений в стоимости благ, должно существовать большое число операций, в которых меновые операции связаны с увеличением или уменьшением стоимости» ([1], стр. 24).

В этом случае из основного уравнения А - П = К получаются теперь такие уравнения:

а) Продажа товара, имеющего покупную стоимость а, по продажной стоимости а + пр:

А - а + (а + пр) - П = К + пр.

б) Выход блага а с убытком у (вместо а получается а - у):

А - а + (а - у) - П = К - у.

Пермутации и модификации

Я.В. Соколов относил И.Ф. Шера к авторам «философской теории двух рядов счетов», называя в их числе помимо автора «Бухгалтерии и баланса» ([1]) швейцарского автора Фридриха Гюгли (1833-1902) и отечественных бухгалтеров - Георгия Авксентьевича Бахчисарайцева (1875-1926) и Николая Севастьяновича Лунского (1867-1956).

По мнению Я.В. Соколова, объединяет этих авторов убеждение в том, что «дебет и кредит - абсолютно условные понятия, подобные меридианам и параллелям на географических картах» ([2], стр. 257).

«Такой подход, - по мнению профессора Я.В. Соколова, - означает, что если мы учитываем нечто в двух группировках (актив и пассив), то для поддержания постоянного равенства между этими группировками мы должны непременно делать две записи каждого факта хозяйственной жизни» ([2], стр. 257).

«Это направление, - пишет Я.В. Соколов, - получило название балансовой теории, так как его представители выводили двойную запись из балансового уравнения» ([2], стр. 258).

Общим для взглядов «сторонников балансовой теории», как считает профессор Соколов, является утверждение того, что «в основе всех бухгалтерских процедур лежит равенство

А = П, где

А - множество, именуемое актив, П - множество, именуемое пассив. (Названия условны, их можно поменять местами.)» ([2], стр. 258).

«Эти множества, - пишет Соколов, - ... могут меняться в сторону увеличения и в сторону уменьшения, но ... может меняться и только структура каждого множества. Изменение объема обоих множеств получило название модификаций, изменение структуры одного из названных множеств - пермутаций.

Каждое действие и/или событие меняет элемент одного и/или обоих множеств (А и П)... .

Итак, если ... действие и/или событие модифицирует множества, то

А + а = П + а

или А - в = П - в, где

а - факт хозяйственной жизни, увеличивающий оба множества; в - факт хозяйственной жизни, уменьшающий оба множества.

Если действие или событие меняют только структуру одного из множеств, то возможны две пермутации:

А - с + с = П;

А = П + d - d» ([2], стр. 258).

«Эти четыре ситуации, названные А.М. Галаганом ... четырьмя типами, оказали, - пишет Соколов, - серьезное влияние на всю теорию бухгалтерского учета» ([2], стр. 258).

Магическое уравнение

Обретенное осознание балансового равенства как непреложного закона бухгалтерии радовало бухгалтеров, внушая ощущения законченности и совершенства. А = П стало постулатом, вне которого бухгалтерский учет терял всякий возможный смысл. Еще в 1891 году «первый, - по словам Я.В. Соколова, - русский чистый теоретик учета» ([3], стр. 254) Василий Дмитриевич Белов писал:

«Научные принципы тогда только становятся законами, когда находят свою математическую формулу; понятие о тяготении существовало и раньше открытий Ньютона, но оно стало законом лишь тогда, когда Ньютон облек его в формулу. Бухгалтерия как знание, счастлива тем, что ея формула найдена. Точно также и раньше открытия этой формулы люди считали в продолжение долгих веков, но научились считать лишь тогда, когда формула двойного счета была открыта. Раз это открытие было сделано, все существенно изменилось: сама собою явилась стройная система, объединившая все частности; практическое знание, блуждавшее до того во тьме, стало ясным и определенным; все практические вопросы счетоводства нашли свое разрешение, а все частные понятия - капитал, счет, баланс и т. д., получили свои точные определения. Так, счет баланса с самой строгой точностью определился формулой: a = b + c, где a - актив, b - пассив, c - капитал. Отсюда само собою вытекает такое же строгое определение счета капитала, которое представляет не что иное, как разность актива и пассива баланса. Это уравнение дает возможность строить различные частные случаи, а которых a > b, a < b, b > c, b < c, и т. д. Во всех этих случаях выводы будут математически верны и дадут практические решения для каждого частного случая» ([4], стр. 211-212).

Подчеркивая законченность знаменитого бухгалтерского равенства, Я.В. Соколов писал, что «упреждая ответы энтузиастов, необходимо прямо заметить», что невозможно помимо двойной записи изобрести тройную, четверную или n-мерную запись, «ибо каждый символ - показатель, отражающий однородное подмножество объектов, учитываемых бухгалтером, может изменяться только или в сторону увеличения, или уменьшения. Таким образом, и теоретически, и практически возможна только двойная запись»* ([2], стр. 257-258).

Примечание:
*  Заметим, что о потенциальной возможности n-мерной записи говорит, например, теория слоев хозяйственных фактов самого профессора Соколова. Согласно данной теории факт хозяйственной жизни, как явление реального мира, может получать n возможных трактовок в n так называемых его слоях - экономическом, юридическом, информационном, временном и т. п. При этом утверждается конгруэнтность слоев факта, что отнюдь не предполагает их тождественности друг другу. Данный подход, в частности, допускает совершенно самостоятельную оценку факта в рамках каждого из n его слоев. Однако возможность представить факт одновременно в n слоях необходимо предполагает отказ и от постулирования балансового равенства и от двойной записи, допускающей отражение лишь равных сумм оборотов по дебету и кредиту счетов.

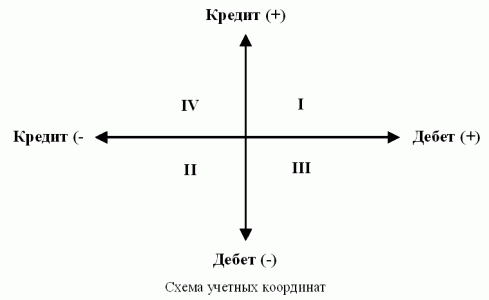
Схема учетных координат Я.В. Соколова

Говоря о теориях двойной записи, Я.В. Соколов отмечает, что из них «самой впечатляющей с логической точки зрения надо признать теорию балансовую» ([2], стр. 259). «Ее формальные достоинства, - по его мнению, - могут быть расширены, и каждый факт хозяйственной жизни должен рассматриваться в этой достаточно полной системе, предусматривающей интерпретацию дебета и кредита как векторов специальной прямоугольной системы учетных координат, которая состоит из четырех квадрантов: I - традиционный: дебет (+), кредит (+) - все операции отражаются положительными числами; II - сторнировочный: дебет (-), кредит - (-) - операции отражаются отрицательными числами; III и IV - смешанные: III квадрант: дебет (+), дебет (-), IV квадрант: кредит (+), кредит (-) - операции отражаются одновременно положительными и отрицательными числами» ([2], стр. 260) - см. схему.

Балансовое равенство со временем стало казаться чем-то настолько естественным, что современные теоретики учета уже не считают нужным его как-то серьезно объяснять. Оно есть, и этого достаточно. Так, например, американские авторы Э.С. Хендриксен и М.Ф. Ван Бреда в своей работе «Теория бухгалтерского учета» ([5]) пишут, что «понятие двойственности, которое так часто используется для оправдания двойной записи, просто требует, чтобы были признаны и отражены в учете две стороны одной операции. Это можно легко сделать как в одной колонке, используя знаки „+" и „-", так и в двух колонках, одна из которых называется „дебет", а другая „кредит". ... Другими словами, весь механизм „дебет - кредит" представляет собой остроумное решение несуществующей проблемы» ([5], стр. 32-33).

Вместе с тем именно арифметическое равенство актива и пассива баланса и сегодня определяет возможности отражения любого хозяйственного факта в рамках финансового учета, итогом которого является составление бухгалтерского баланса компании хозяйствующего субъекта.

В балансе, составляемом сегодня на практике, любое увеличение или уменьшение внеоборотных или оборотных активов, меняющее итог баланса, возможно лишь за счет, соответственно, увеличения или уменьшения капитала и резервов или отражаемых в пассиве обязательств. Иных вариантов в рамках баланса, где А всегда равно П, просто не существует.

Балансовое уравнение и поиск неизвестного

Итак, баланс - это простейшее уравнение, и это во многом определяет его характеристики как бухгалтерской модели предприятия.

Математический энциклопедический словарь определяет уравнение как «аналитическую запись задачи о разыскании значений аргументов, при которых значения двух данных функций равны. Аргументы, от которых зависят эти функции, называют обычно неизвестными, а значения неизвестных, при которых значения функций равны - решениями (корнями) уравнения; о таких значениях неизвестных говорят, что они удовлетворяют данному уравнению» ([6], стр. 603).

В уравнении

Актив - Обязательства = Капитал,

актив, обязательства и капитал выступают в качестве функций уравнения, а финансовый результат - прибыль или убыток - в качестве его неизвестного. И вот уже практически пять веков бухгалтерский учет решает это уравнение, сообщая заинтересованным лицам о прибылях и убытках экономических субъектов.

Если неизвестное балансового уравнения - прибыль или убыток - обозначить за Х, то возможные варианты включения этого неизвестного могут быть представлены следующим образом:

Актив + (-) Х - Обязательства = Капитал + (-) Х, и

Актив - (Обязательства + (-) Х) = Капитал - (+) Х.

Таким образом, в рамках балансовой модели фирмы, прибыль трактуется либо как рост активов при сохранении объема обязательств, либо как уменьшение обязательств при сохранении объема активов. Убыток, соответственно, представляется как уменьшение объема активов без изменения величины обязательств или рост величины обязательств при сохранении объема активов.

Однако, если в математике уравнения - это лишь числа, то в бухгалтерии - это числа, которым вменяется определенный экономико-правовой смысл. При этом числа, получаемые с помощью оценки в деньгах неденежных экономико-правовых объектов, формирующих активы и пассивы предприятий.

В статическом балансе решение его уравнения предполагало трактовку прибыли как увеличения богатства собственников фирмы, выраженное в деньгах. В динамическом - прибыль понималась как разность между суммами денежных средств, потраченных и полученных в процессе кругооборота капитала фирмы.

И в первом, и во втором случае суммы денег выполняли лишь счетную роль, однако деньги - это не просто числа, а числа с определенной покупательной способностью, которая постоянно меняется во времени. И развитие экономики делает эту их особенность все более и более заметной.

Если в математике, допустим, число 2 всегда больше числа 1, то в экономике 2 рубля «сегодня» могут оказаться меньше, чем рубль «вчера». И не учитывать это обстоятельство - значит формировать недостоверную экономическую информацию.

Теория Ф. Шмидта и арифметика бухгалтерского баланса

Фриц Шмидт (1882-1950) попробовал решить эту проблему. Однако, его идея ввести в баланс восстановительные оценки не вписалась в простую балансовую арифметику, задаваемую равенством А = П.

Давайте вспомним наш классический пример. Фирма купила партию товаров за 100 000 руб. и продала их в розницу за 120 000 руб. Можно констатировать, что прибыль от осуществленных операций составила 20 000 руб. Однако на момент исчисления данного финансового результата от продаж известно, что цена такой партии оптом составляет уже 110 000 руб. Возникает вопрос: прибыль фирмы в данном случае составит 20 000 руб. или все же 10 000 руб.? Возможны различные варианты трактовки данной ситуации. Одна из них состоит в том, что прибыль - это показатель, свидетельствующий о возможности расширения масштабов деятельности фирмы за счет реинвестирования прироста ее капитала или изъятия его соответствующей части из оборота компании без ухудшения состояния ее дел, в сравнении с тем, которое имело место на начало периода, за который мы исчисляем прибыль.

Именно такой подход, при котором в нашем случае прибыль будет исчислена как 10 000 руб., и предполагал Ф. Шмидт. Давайте посмотрим, насколько это возможно реализовать при составлении бухгалтерского баланса, определяемого арифметическим равенством А = П.

Допустим, что наш баланс на начало осуществления рассматриваемых операций имел следующий вид:

Баланс 1

 Приобретение нами первой партии товаров за 100 000 руб. отразится как пермутация по активу, и наш баланс примет следующий вид:

Баланс 2

Признание в качестве результата операций по продаже товаров за 120 000 руб. прибыли в 20 000 руб. в данном случае соответствует теориям и статического, и динамического баланса.

Теория статического баланса говорит нам о том, что объем имущества фирмы, свободного от долгов, после продажи составил 120 000 руб., а до продажи составлял 100 000 руб. Следовательно, прибыль составляет 20 000 (120 000 - 100 000) руб.

Теория динамического баланса определяет прибыль в 20 000 руб. как превышение величины полученного от данных операций капитала (Д`) над величиной капитала вложенного (Д). Д в нашем случае составляет 100 000 руб., а Д` - 120 000 руб.

Таким образом, и статический, и динамический баланс в нашем случае будут иметь следующий вид:

Баланс 3

Данный баланс можно рассматривать как результат решения уравнения

Активы - Обязательства =

Капитал + Х,

где активы равны 120 000 руб., обязательства равны нулю, капитал равен 100 000 руб., а искомое Х - прибыль - составляет 20 000 руб.

Согласно Шмидту, с целью откорректировать прибыль с учетом роста восстановительных цен товаров мы должны оценить их в 110 000 руб., что позволит определить величину прибыли как не 20 000 руб., а 10 000 руб., то есть 120 000 - 110 000.

В рамках бухгалтерского баланса и двойной записи на счетах как следствия балансового равенства для этого следует переоценить товары, доведя их оценку до 110 000 руб. Однако балансовое равенство предполагает, что такую переоценку активов мы можем сделать либо за счет увеличения отражаемой в пассиве кредиторской задолженности (а обязательства в нашем случае не меняются, поэтому данные вариант невозможен), либо за счет увеличения оценки собственных источников средств. В последнем случае балансовое равенство предполагает, что, переоценив товары в сторону увеличения их стоимости и не увеличив при этом оценку кредиторской задолженности, мы покажем увеличение капитала фирмы, то есть прибыль.

Баланс в этом случае примет следующий вид:

Баланс 4

Однако, согласно теории Шмидта, рост восстановительной стоимости товаров в данном случае, наоборот, означает уменьшение прибыли, а, следовательно, баланс должен иметь следующий вид:

Баланс 5

Однако итоги актива и пассива такого баланса становятся не равны между собой, и, следовательно, арифметическое балансовое равенство и метод двойной записи не позволяют нам реализовать идею Ф. Шмидта. Иными словами, Шмидт предложит «решать» бухгалтерский баланс как уравнение:

Активы + Х - Обязательства

= Капитал - Х

В нашем случае, такое равенство принимает следующий вид:

100 000 + Х = 100 000 - Х

Оно имеет единственное решение: Х = 0, но такое решение нам никак не подходит.

Отсутствие иных вариантов решения балансового уравнения по Шмидту и обусловило то, что теория органического баланса не получила воплощения в практике ведения финансового учета.

Однако это не отменило стоящих перед бухгалтерским учетом методологических проблем, связанных с необходимостью представления в отчетности и, прежде всего, в балансе влияния на положения дел фирмы динамики покупной способности денег во времени.

Забавное настоящее и туманное будущее

Заканчивая эту статью, хочется процитировать наших известных американских коллег Э.С. Хендриксена и М.Ф. Ван Бреда: «С тех пор, как 500 лет назад Пачоли написал свою книгу, бухгалтерский учет, в сущности, остался неизменным. Наверное, Лука Пачоли чувствовал бы себя комфортно при существующих учетных системах.

Ему было бы несложно понять и новые финансовые инструменты, которые поначалу, может быть, его и озадачили бы. Но, выслушав один раз объяснения, что это всего лишь новые формы кредита, которые следует показывать в правой части баланса, он в дальнейшем не имел бы никаких трудностей понимания.

Между тем в мире произошла информационная революция, которая радикально должна была бы повлиять и на учет. Сейчас мы наблюдаем нечто похожее на то, что было во времена промышленной революции, когда использование технических достижений отставало во времени от их изобретения. Авторы учебников все еще объясняют, как дебетовое сальдо показывать с левой стороны, а кредитовое с правой, учат студентов технике вычитания меньшей противоположности, которая еще три века назад была признана арифметически устаревшей. Программисты старательно отражают эти средневековые идеи на экране компьютера. Бухгалтерскому учету еще предстоит адаптировать новые изобретения, которые трансформируют финансовую отчетность» ([5], стр. 37).

Интересной попыткой такой «адаптации» современных экономических знаний является бухгалтерский баланс, составляемый в соответствии с положениями МСФО. О нем наша следующая статья.

Литература:

1. И.Ф. Шер. Бухгалтерия и баланс -

2-е изд. / пер. с нем. Под ред. Н.С. Лунского - М.: Экономическая жизнь, 1925.

2. Я.В. Соколов. Основы теории бухгалтерского учета - М.: Финансы и статистика, 2000.

3. Я.В. Соколов. Бухгалтерский учет: от истоков до наших дней - М.: ЮНИТИ, 1996.

4. В.Д. Белов. Бухгалтерия и математика // Счетоводство № 16 - 17, 1891.

5. Э.С. Хендриксен, М.Ф. Ван Бреда. Теория бухгалтерского учета - М.: Финансы и статистика, 2000.

6. Математический энциклопедический словарь - М.: Большая российская энциклопедия, 1995.